|
|
|
|
|
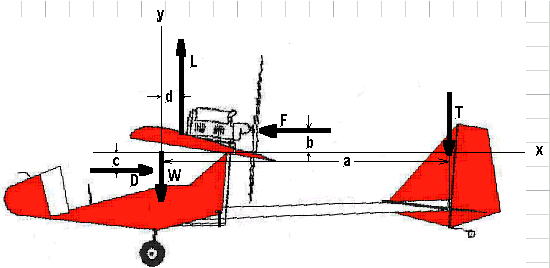
Since I am able to lower the thrust line by rotating the Victor 1+ belt reduction unit, I have become curious as to what effect it would have on pitch trim. As I have lowered the thrust line, it seems that the cruise speed noise level has decreased. I put together the above diagram so that I could solve for L or Lift in the general case. Then by substituting in various dimensions and loads (forces) to determine their effect on Lift or wing load and tail load at cruise.
The dynamic analysis goes like this.
Sum of Forces in x -> 0=D-F therefore D=F The Weight force passes through the CG. To minimize the moment effect of CG location with the center of Lift, I chose to use the most to the rear CG of 37%. I have no idea where the center of drag would be, but I assumed that it was below the trailing edge of the wing. The same is true of the Lift force. I put it displaced it back from the CG to ensure that the FireFly would be stable. The thrust Force was computed using JAVAPROP while assuming the Victor 1 was putting out 38 hp at 5200 rpm with a 2.7 ratio belt reducer driving a 56 inch diameter propeller pushing the FireFly 63 mph.
The perpendicular distances measured/calculated/estimated:
Other assumptions: Putting all values in but thrust line height b gives:
L=508+1.053•b# With belt reducer set at 0 degrees:
L=524#
|
 With belt reducer set at 135 degrees:
With belt reducer set at 135 degrees:
L=514# This indicates that for every inch one lowers the thrust line one pound comes off the wing and the same comes off the horizontal tail. Dropping the thrust line by rotating the belt reduction unit from zero degrees to minus 135 degrees reduces these loads by 9.9 pounds. If one moves the CG to the forward wing chord limit of 20% and the center of lift remains in its original position, the lift and tail forces will increase by an additional 18 pounds. Because the FireFly is so dragy, the thrust force given by JAVAPROP may be conservative. If this is true, then the actual L & T values will be higher than estimated above. |