parasitic drag article

Parasite Resistance, Struts And Wires

This article was taken from EAA AIRCRAFT DESIGN, Volume 3, Copyright 1970, page 53 *************************************************** Parasite Resistance, Struts And Wires By Ken Kuhn, EAA 15054 9208--48th P1., College Park, Md. HAVE YOU ever said to yourself ..."I wonder how much drag there would be if I installed this instead of that in my airplane?" If you have pursued this past the wondering stage, you have probably confidently opened a fluid dynamics text looking for an easy solution only to find that you were zapped with Reynolds numbers, viscos- ity coefficients, temperature and pressure variations and, most times, reams of integral calculus. After the initial shock you then probably slowly closed the book and said . . . "I wonder how much drag there would be if I in- stalled this instead of that in my airplane?"

The mathematics behind these drag computations are, without question, complicated, and there must be an easier way. Well, there is an easier way, that is, if you are not building an aircraft that will reach Mach .9 or have a 50,000 ft. ceiling. The average amateur-builder will have a craft in the 100-125 mph class and will stay below 5,000 ft. The mathematics presented here will be valid within reasonable variations of these limitations.

With this in mind, let us consider the drag forces on round tubing, solid round wire, stranded round wire, streamlined wire and streamlined tubing. In all the cate- gories mentioned, the drag force is directly proportional to the diameter and length of the member, and the square of the velocity of that member (within the stated limitations). Algebraically: F=kDLV² (eq.-1) Where: F = drag force in pounds D = "frontal" diameter of the member in inches L = overall length of the member in feet V = airspeed of member in mph k=constant of proportionality (this will vary with the shape of different members). 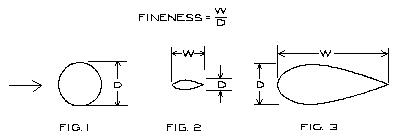The following table is for various values of k, depending upon the shape of the member: =========================================================== TABLE I ----------------------------------------------------------- Fig. 1 Round tube & solid round wire, dia. = .125 in. & larger ............k = .00026028 Round tube & solid round wire, dia. = less than .125 in ............k = .00022124 Stranded wire ..........................k = .00030976 ----------------------------------------------------------- Fig. 2 Streamlined wire, fineness 4, dia. = .10 in. & larger .............k = .00008906 Streamlined wire, fineness 4, dia. = less than .10 in .............k = .00008497 ----------------------------------------------------------- Fig. 3 Streamlined tubing, fineness 2.0 .......k = .00002366+ Streamlined tubing, fineness 2.5 .......k = .00001940 Streamlined tubing, fineness 3.0 .......k = .00001798 Streamlined tubing, fineness 3.5 .......k = .00001747 Streamlined tubing, fineness 4.0 .......k = .00001710 Streamlined tubing, fineness 4.5 .......k = .00001647* ===========================================================

The fittings to which the ends of the struts, wires, etc. are attached sometimes extend out into the air somewhat, and add to the total resistance. It is almost impossible to calculate the effect of these fittings, consequently only rough approximations can be made. The following notes are given in connection with the table of resistances of struts and wires.

NOTE I: For the resistance of cables and wires, add one foot to the length of cable for the turnbuckle, and one foot for the eye and fitting. NOTE II: For the resistance of streamlined wire, add one-half foot to length of wire for simple fork ends. Neglect resistance of end fittings if incidence wires are attached directly to the strut socket. NOTE III: For total resistance of struts, use total length, including the space occupied by sockets and fit- tings, and add three feet per strut for the additional re- sistance of the two end fittings. All right, now we have the drag force on the wires and struts but, to make good use of this knowledge, we should equate this to the amount of power required to overcome this resistance. To put it another way "how much hp is this going to cost me?" The formula for this is as follows: HP = FV (eq.-2) 375 Where: F = drag force in pounds V = airspeed in mph. Combining eq.-1 with eq.-2, we obtain: HP = kDLV³ (eq.-3) 375 Here is an interesting point, although it gets away from the subject a bit. Notice how the hp varies with the cube of the velocity. Let's take an example of an air- craft which requires 100 hp to attain a speed of 150 mph, and see what requirements exist for the same aircraft at higher speeds, assuming that the parameters of the prob- lem do not change (i.e., neglecting boundary layer theory, compressibility, temperature and pressure variations, etc.). ============================================================ TABLE II ------------------------------------------------------------ Mph Hp 150 100 200 240 300 800 400 1900 =========================================================== So, if you are thinking of building a real sizzler, re- member that not only does the hp requirement vary with the cube of the velocity, but so also does the gas bill. References:

1. "Simple Aerodynamics" by C. C. Carter (Ronald Press Co., New York. 1942) 2. "Vol. 1, Navy Design Data" (Incorporated in above text). -------------------------------------------------------- Corrections and Additions + I added this line. * Using interpolation, I changed the number from .00001747